公司新闻
对规范风荷载计算的思考和解读(上)——献给不盲从规范,而寻求利用自然规律的工程师
前段时间跟L君做项目的时候,跟他讨论起规范风荷载计算的事情。
他说规范计算公式参数太多,特别是横风效应,不好理解背后的原理,然后他知道我本身学抗风的,就叫我看一下,看能不能解读规范风荷载计算的原理。然后刚毕业的我当然老老实实仔仔细细地看了,看完之后,果真发现了许多东西,不断做笔记,感觉在读规范的同时,也对自己结构抗风知识有了一次提升。
总的来说,规范风荷载计算部分其实就是在大量风洞实验数据的基础上加以归纳和总结出来的,在这里跟大家分享一下自己读规范所得和一些思考,有不对或不严谨的地方,欢迎指正~
引用结构大师林同炎的一句话:
献给不盲从规范,而寻求利用自然规律的工程师。
2-1 计算公式
顺风向计算主要有两个公式,一个用于计算主体结构受力,另一个用于计算围护结构,公式的形式相似,差别就在于采用不同的风振系数和体型系数。这样做是因为围护结构如幕墙的设计需要考虑风压在建筑表面分布不均匀的情况,所以采用的是局部的体型系数。计算主要受力结构公式如下:
大家都知道, 为风振系数,
为体型系数,
为高度变化系数。很明显,其思路是先通过基本风压乘以高度变化系数把10m高度的风压转化为各高度上的风压,然后乘以体型系数得到不考虑动力效应下建筑物表面的风压,再乘以风振系数最后得到考虑动力学效应后的最大压强。下面对各系数分开讨论。
2-2 高度变化系数
首先我们可以看到规范给出了以下表格:
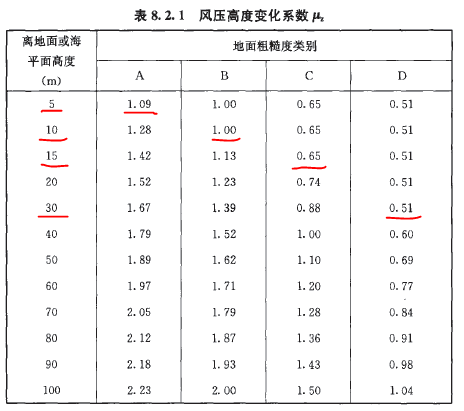
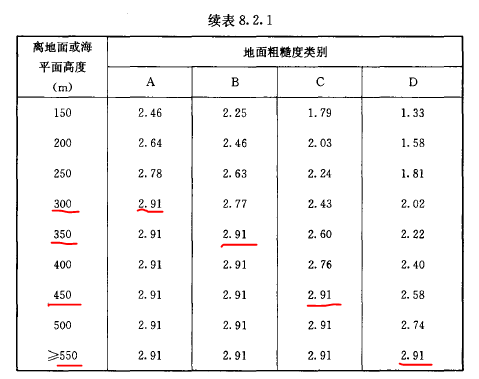
从表格可以看到高度变化系数下有截断高度,上有梯度高度,截断高度以下和梯度高度以上系数取定值。这里要注意的是在各地貌梯度高度上的高度变化系数相等,也就是说在同一地区选取同样的基本风压的条件下,不同地貌的梯度风高度风速是相等的。其中A,B,C,D地貌的梯度高度分别是300m,350m,450m和550m。同时规范条文说明也给出了以下公式:
现在统一记为 ,其中α就是不同地貌下风剖面的指数,K跟地貌有关,把这个表达式带入到风压计算公式中可得:
其中记 ,显而易见这个正是各类地貌下的风剖面,
为地区基本风压换算而来的风速,故为该地区10m高度处的风速,故不同地区基本风压下的各地貌下的风剖面公式可写为:
其中 (空气密度按1.25算),根据规范公式K按下面表格取值(对上面高度变化系数公式的系数取根号):

看到这里,可以发现,在B地貌下,K=1,也就是说基本风压是在B类地貌的情况下测量而来的,基本风压换算得来的风速就是B类地貌10m高度风速。
至于高度变化系数公式的系数,也就是K值的计算由来,到这里其实显而易见,就是通过在B类地貌K=1的前提下,根据不同地貌的梯度风高度风速相等的条件计算得来。例如由 得:
,进而得到:
其他地貌K值类似。为得到更直观的比较,下图给出了不同地貌下高度变化系数随高度变化图(也就是风剖面的形状):
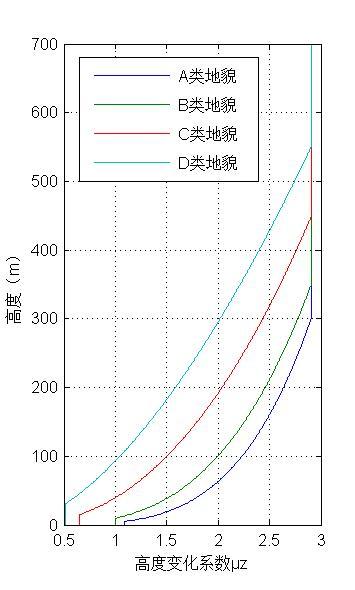
显然,A,B,C,D地貌同一高度下风速递减,风剖面变陡,截断高度和梯度高度变高。
2-3 体型系数
关于体型系数规范给出了很清晰的定义,即风作用在建筑物表面一定面积范围内所引起的平均压力(或吸力)与来流风的速度压的比值。体型系数和局部体型系数的区别就在于这个面积的范围,一般地,体型系数给出了建筑物某个面整个面的平均压力的比值,而局部体型系数进一步深化,把建筑表面划分为几个区域分别给出风压的比值。体型系数的大小跟固体和流体相互作用有关,十分复杂,规范只给出了典型形状建筑物的体型系数,对于其他复杂形状的建筑应由风洞实验确定。
从规范的体型系数表格可以得出一些简单规律,对建筑外形设计有一定指导作用,以下只列出几条(其实现在已经有许多专家和学者在研究气动外形优化这个课题,特别对于超高层建筑设计尤为重要)
1)低矮房屋通过对屋盖倾斜度的调整,可以有效降低体型系数以减少风荷载。如规范体形系数表格第27条,如下图:
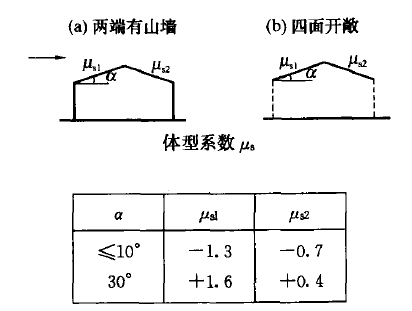
通过对角度α的调整,大概在20几度时,体型系数将接近于零。
2)建筑平面出现凹进去的情况,体型系数增大,对抗风是不利的,设计时应该考虑到。同样我们可以看到表格第30条:
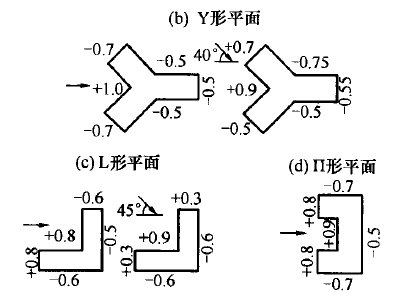
3)对于高层建筑,随着深宽比的减少,背风面体形系数增大。故高层建筑设计得过于“扁平“,不但对侧向刚度有所影响,背风面的吸力也会增大。表格第31条:
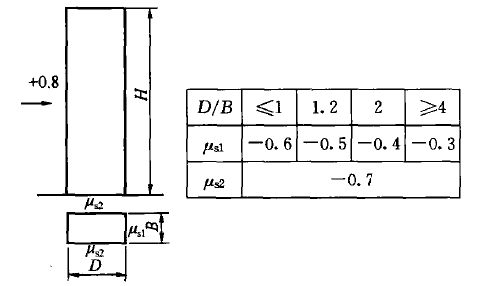
更多的规律读者可以自己进一步探索和查看更多的文献。
值得一提的是,体型系数只会影响表面风压,然而建筑外形不仅影响体型系数,更重要的是会改变其漩涡脱落频率,改变横风向和扭转风荷载,对不同自振频率的结构造成影响,这方面会在下节横风效应讨论。
2-4 风振系数
之前的一篇文章 超高层建筑结构是如何抗风的?——结构风工程入门参考 第三节对风振作了介绍,在风的作用下顺风向结构主要发生抖振。引入风振系数的作用就是为了考虑抖振的影响,其实质是通过随机振动理论计算出建筑结构顺风向风振响应的最大值与平均风作用下的响应的比值。规范条文说明也给出了公式:
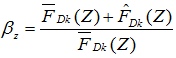
它是以力的方式给出了,式中分子即为平均风荷载与脉动风荷载之和,也就是由风振响应最大值求得的等效静风荷载。分母即为平均风荷载。
这里简单介绍一下等效静风荷载的计算方法。在对结构进行完风振响应分析之后,我们得到了结构的最大位移响应,然后用最大位移响应向量乘以结构的刚度矩阵即得到等效静风荷载。同样在上一篇文章提到过最大位移的公式为:
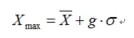
Xmax等于平均响应加上脉动响应的均方根乘以峰值因子g。
等效静风荷载可分为两部分进行计算,即平均风荷载+脉动部分的等效静风荷载。用平均位移乘以刚度矩阵即得到平均风荷载,平均位移可把平均风荷载利用静力方法求出。而脉动位移通过随机振动方法求出,但在计算时一般只会采用前面几阶振型。下面简单讲一下脉动部分的等效静风荷载的求解:
由结构动力学我们得到:
当仅考虑一阶模态时,带入上式故进一步得:
,当脉动位移最大时,得到:
所以即为脉动部分的等效静风荷载。
现在我们再来看看规范给出的脉动风荷载公式:
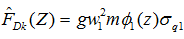
我更愿意把它写成下面这个形式:
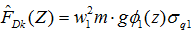
m为单位高度上的质量,上式实际上就是上面所说的 ,即脉动等效静风荷载。
由上面公式可知,求解等效静风荷载关键是要得到一阶广义力的均方根 ,那它是怎么样求得的呢?
是这样的,一般由高频底座天平实验(HFFB,风洞实验的一种)得到结构的基地弯矩时程,然后这个弯矩除以建筑高度在线性振型下实际上就是广义力,然后对其求谱乘以频响函数再进行积分开方,便得到广义位移均方根 。当然你也可以直接求出响应时程求均方根,但是通过频域的分析可以更好地知道风荷载在频域上的表现,而且规律性更强,而规范正是对大量风洞实验数据频域分析的基础上推导出顺风向
的公式。
规范的公式是怎么得出的呢,具体推倒我无从得知,只说说大概原理。下图给出了典型的顺风向脉动响应功率谱的情况:
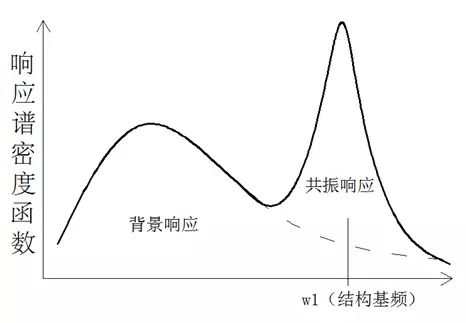
通常把功率谱分为背景响应和共振响应两部分,背景响应与结构自振频率关系不大而与风场自身的湍流强度,建筑迎风面积等有关。而共振响应顾名思义则是顺风向脉动风荷载与结构发生共振而产生的部分,故与结构自振频率密切相关。规范的计算正是对这两部分分别定义了背景响应分量因子 和共振响应分量因子R来表示。
现在我们回到风振系数的公式:
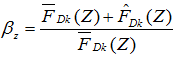
应该大概知道它的由来了吧。
=========================================================================
顺风向风荷载计算总算写完,但不知不觉写了这么多,然而还没开始横风向风荷载计算的部分,Aaron还有很多话要说,然而现在还有其他的事情来不及写,所以决定把文章分为上下部。以上为对顺风向风荷载计算的一些思考和想法,下半部分将对规范横风效应和风振加速度计算方法进行探讨,敬请期待~ (可能又要半个月后了,最近聊天都没时间,囧)
由于Aaron才疏学浅,有不对或不严谨的地方,敬请指出和讨论~
欢迎关注知乎专栏
想了解更多?推荐阅读:
2. 什么样的超高层设计才是好的设计?——关于超高层建筑抗震和抗风的一点思考
扩展阅读:
8A新闻
联系我们
公司名称: 8A-8A娱乐-注册登录商务站
手 机: 13800000000
电 话: 400-123-4567
邮 箱: admin@youweb.com
地 址: 广东省广州市天河区88号

