公司新闻

拓扑相变

最近了解了拓扑相变，这个内容蛮有价值的, 想浅浅写一些对拓扑相变、凝聚态物理中的拓扑应用的理解。有幸读了戴希教授的文章《凝聚态材料中的拓扑相与拓扑相变——2016年诺贝尔物理学奖解读》, 顾险峰教授的文章《高山仰止-从微分几何角度浅谈陈省身示性类》，以及其它一些关于拓扑相变的参考文献，下面内容的部分观点取自以上内容。接下来分四部分阐述：

一、2016年诺贝尔物理学奖

二、拓扑相变

三、整数量子霍尔效应

四、绝缘体的分类

一、2016年诺贝尔物理学奖

2016年，诺贝尔物理学奖授予 David J. Thouless、 F. Duncan M. Haldane 和 J.Michael Kosterlitz ，以表彰他们对“物质的拓扑相变和拓扑相的理论发现”。

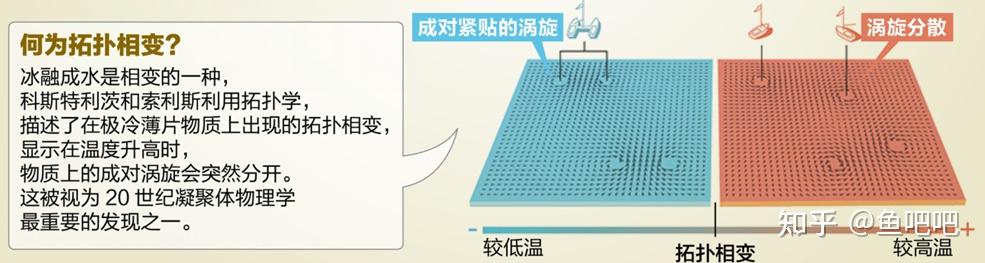
关于拓扑相和拓扑相变，Thouless、 Haldane 和 Kosterlitz 主要做了哪些工作呢？20世纪70年代早期，当时的理论认为超导现象和超流体现象不可能在薄层物质中产生，而 Kosterlitz 和 Thouless 推翻了这一理论。他们证明了超导现象能够在低温下产生，并阐释了超导现象在较高温度下也能产生的机制——拓扑相变。 20世纪80年代，Thouless 与合作者指出整数量子霍尔电导效应可以用拓扑中的陈数来解释。Haldane在二维量子材料中研究拓扑相及其转变，1988年，他提出无需强磁场在晶格体系中也可以实现整数量子霍尔效应，为后来的量子反常霍尔效应和拓扑绝缘体的研究提供了理论基础。

二、拓扑相变

20世纪70年代早期，Thouless、Kosterlitz提出二维超导和超流性质的新模型，并解释温度的变化会导致超导体或超流体发生相变。这种相变被称为拓扑相变，也叫BKT相变（Berezinskii–Kosterlitz–Thouless transition）。极低温度下，超导/超流薄层物质中的涡旋成对出现(手性相反)，波函数相位呈现“准长程序”束缚态，伴随超导或超流现象；温度升高到一定值后，成对涡旋分散开来，开始做自由无规则运动，薄层物质发生相变。这种相变不同于普通的伴随对称性破缺的相变，波函数相位由准长程序变为无序，手性相反的成对束缚态涡旋变为无序运动的自由态涡旋。

上面的解释中涉及到相、相变、对称性破缺、波函数、涡旋等专有名词，以下是对它们的一些注释：

相：物质系统中物理性质完全相同，与其他部分有明显分界面的均匀部分称为相。

例子：水、冰组成的系统中，水是一种相，冰是一种相，雪花不同的结晶态有不同的相。

相变：物质从一种相转化为另一种相的过程，是物理过程。

例子：水变成冰。

对称性破缺：物理学中，一个作用于系统的小扰动使系统跨越临界点，通过某个确定去向来决定系统最终状态，称此现象为对称性破缺。

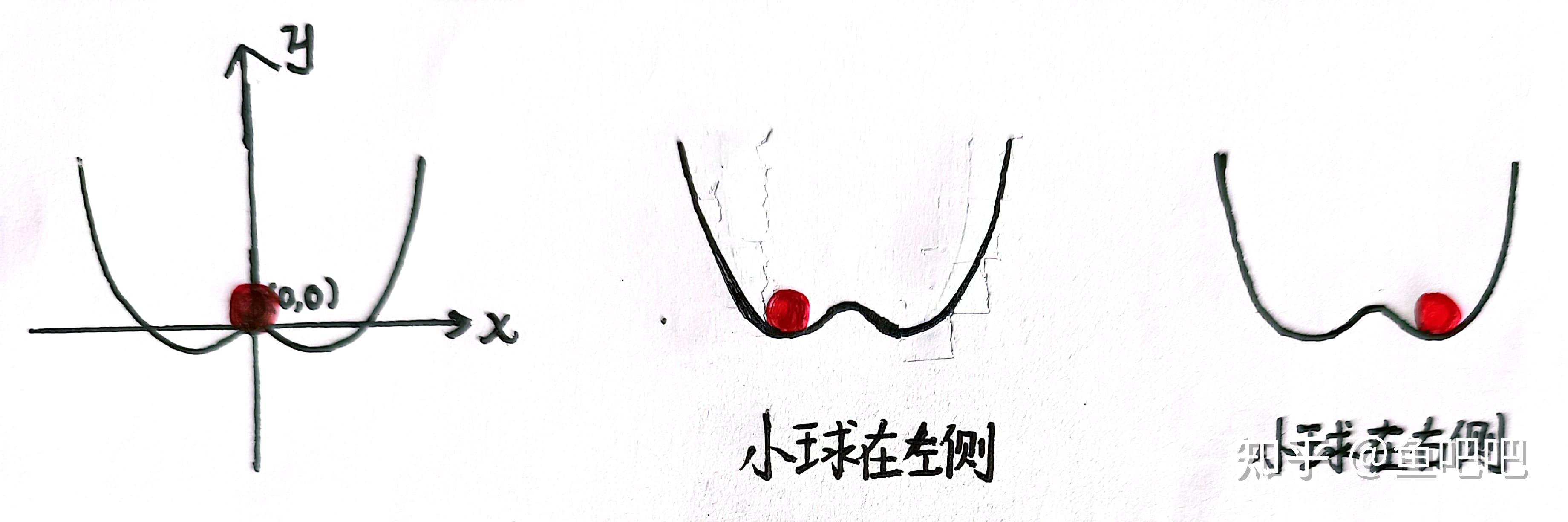
例子：系统初始状态时，在原点放置一个小球，此时系统对称，但对系统施加小扰动后，不管最后小球落到左侧还是右侧，观察者观察到的最终状态都是不对称的，因此系统的对称性被破坏。

普通相变：有对称性破缺

例子：冰升温时变成水；液态水银在极低温下变成超导体；

解释：固相原子排列有序，有严格的周期性，但其他原子位于某个原子周围的几率是各向异性的，固相原子在结构上对称性较低；液相原子排列无序(略去短程有序)，在每一原子周围，距原子相同距离的各个位置上，其它原子占据此位置的几率相同，液相原子在结构上有较高对称性。

拓扑相变：没有对称性破缺

例子：极低温超流/超导体升温过程中发生的相变，存在涡旋运动；

波函数：描述电子在空间分布概率的复函数。一般形式为 $\\psi(x,t)$ ，描述 $t$ 时刻在点 $x$ 附近单位体积内发现粒子的概率。

物质由分子或原子构成，原子由原子核和电子构成，电子绕原子核作无规则运动。电子在空间中个点出现的概率像一个波，用波函数来描述。波函数有相位(也称相位角)，因此物质中电子波函数在各点的相位构成相位空间。对一个超流/超导体而言，它的相位空间 $\\left\\{ \ heta(x,y) \\mid (x,y)\\in R^2,\ heta\\in[0,2\\pi],0\\sim2\\pi\\right\\}$ 是一个紧致闭空间。如果用以某点为起点的有向箭头表示此点的相位方向，那么超流/超导体的电子的波函数相位空间中可产生涡旋。

涡旋、反涡旋示意图：

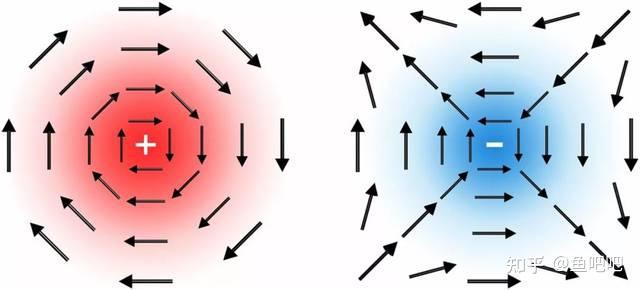
普通相变和BKT相变可以用拓扑来区分。BKT相变的涡旋相位空间不能连续形变到普通相变的无涡旋相位空间，而一个空间连续形变另一空间可以推广为一个拓扑空间同伦等价于另一拓扑空间。因此两种相位场属于不同的拓扑类。

三、整数量子霍尔效应

1980年冯·克利青（Von Klitzing）等人首先观测到了量子化的霍尔效应。在将一薄层物质放入两个半导体之间，在极低温度强磁场下，薄层物质的霍尔电导率不再连续变化，而是以整数倍变化，出现量子化平台，观测到量子化电导= $e^2/h$ 。在此之前，所有在凝聚态体系的物质状态均可以用对称性破缺原理来描述，而量子霍尔效应是第一个不存在自发对称性破缺的量子态。

Thouless等人对整数量子霍尔效应的解释：

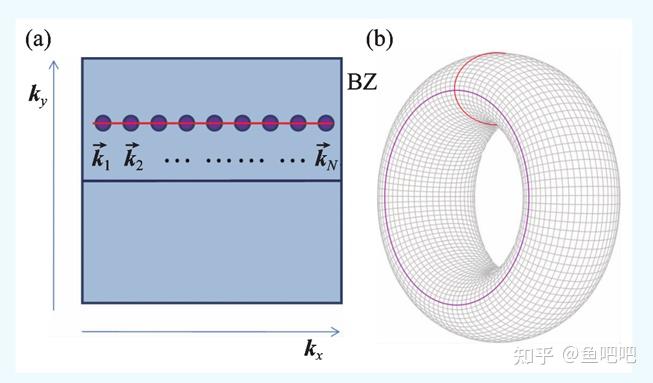
对于一个无电子相互作用的绝缘体，考虑一无限大的二维晶格上的一般形式的周期势场，外加一个垂直于平面方向的均匀磁场。假设每个元胞内的磁通量是有理数(磁通量子为h/e)，波函数的相位是任意的。粒子的动量在空间有位置分布，二维动量空间构成布里渊区，由于动量在空间中具有周期性，则布里渊区上边缘和下边缘的动量相等，左边缘和右边缘的动量也相等，则布里渊区上下边界等价，左右边界等价，二维布里渊区就等价于一个环面(Torus)。将布里渊区看作底流形，布里渊区上的单电子波函数连同底流形构成一个U(1)主丛。根据线性响应理论，霍尔电导可表示为Berry曲率在整个布里渊区(环面)上的积分，这个积分就是此U(1)主丛的陈示性数(Chern number)。

上面的解释中涉及到布里渊区、纤维丛、陈类等专有名词，以下是对它们的一些注释：

能带理论：讨论晶体中电子状态及其运动的一种重要的近似理论。它把晶体中每个电子的运动看成是独立的在一个等效势场中的运动。

布里渊区：在能带论中，固体的各种电子态按照它们的波矢分类。在倒易格子中取某一倒易阵点为原点，作所有倒格矢的垂直平分面，倒易格子被这些面划分为一系列的区域：其中最靠近原点的一组面所围的闭合区称为第一布里渊区。

纤维丛：

纤维丛例子：

陈数：陈数是一个微分几何概念，陈数基本上可以看成是一些外微分形式在流形上的积分，是一种拓扑不变量。

设 $S$ 是一紧致无边的二维黎曼流形,令 $K$ 为的高斯曲率， $dA$ 为曲面面积元。由于曲面切丛的陈类可以表示为二阶微分形式 $KdA$ , 根据 $Gauss-Bonnet$ 定理，陈类在曲面上的积分给出欧拉示性数

$\\frac{1}{2\\pi}\\int_{S}^{}KdA=\\chi(S)$

四、拓扑绝缘体的分类

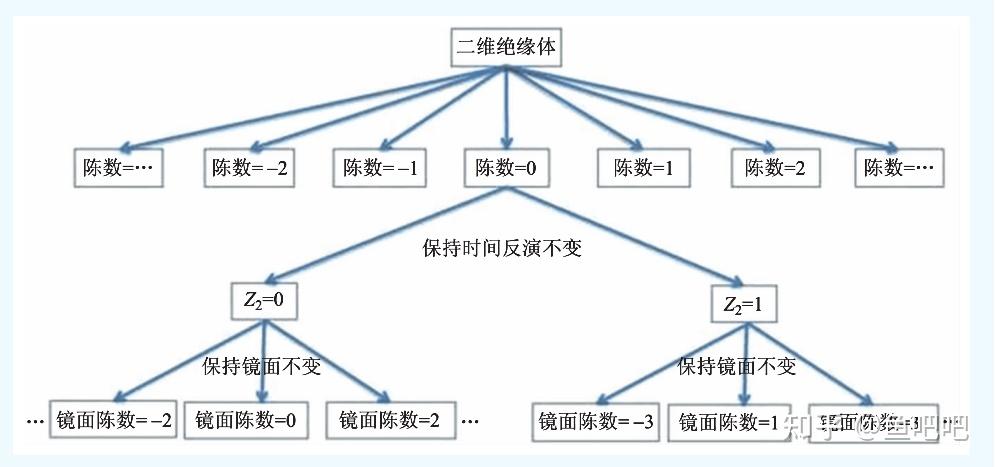
陈数分类：对破缺时间反演对称的系统，波函数相位是随意的，但是我们可以找到规范不变量。将二维布里渊区按照不同的 $k_y$ 切成一条条的横线，并且在每一条线上按照一定的间距分成 $N$ 个点，可以证明，把相邻 $k$ 点的占据态波函数求内积再乘起来所得的量就是规范不变的。随着 $k_y$ 变化一圈，相位角 $θ(k_y)$ 必须在布里渊区的轮胎面上绕整数 $C$ 圈，这个整数 $C$ 就是 $TKNN$ 发现的陈数。对于二维布里渊区，布里渊区内的动量具有周期性，因此动量空间布里渊区的上边界和下边界等价，左边界和有边界等价，布里渊区等价于环面，布里渊区(底流形)连同布里渊区上的电子波函数构成纤维丛，再对整个布里渊区上的电子波函数进行积分，根据 $Gauss–Bonnet$ 定理，得到的数是2π的整数倍,这个整数就是陈数。不同类的绝缘体对应不同的陈数，于是根据陈数，就可以对绝缘体进行分类。

$Z_2$ 拓扑不变量分类：对具有时间反演对称的系统，它们的电子态由两个互为时间反演态，并且相互之间无耦合的子系统组成，不妨分别记为 A 和B。由于时间反演对称，两个子系统的总陈数为零，但它们各自的陈数可以不为零，而是符号相反的两个整数，比如(1,－1)或者(2,－2)。这种“半个系统”的陈数叫作自旋陈数，比如刚才提到的(1,－1)系统，其自旋陈数就等于1。并且当自旋陈数不等于零时，系统就相应地具有自旋霍尔效应。把二维布里渊区划分成一条条的平行线，与破坏了时间反演对称的绝缘体不同的是，当具有时间反演对称时，最简单的绝缘体系统将至少具有两条占据能带。可以得出结论，在半个布里渊区的相位角演化有两种拓扑上不等价的构型——分别环绕半个布里渊区柱面奇数和偶数圈，奇数圈对应拓扑绝缘体而偶数圈对应普通绝缘体。与陈数分类不同，这种分类在数学上是奇偶类而非整数类，因此称为Z2 拓扑不变量。具有时间反演不变的二维绝缘体就可以分为奇偶两类，其中奇数类具有被时间反演对称保护的狄拉克型边缘态，而偶数类则没有这种受保护的边缘态。