【机器学习】优化器之Adam

? ? ? ?上一个章节说了SGD和动量版本的SGD，这个优化算法目前也是比较常用的一个优化算法，但是它还是存在一些问题的，因此后面又出了几个不同的算法，比如AdaGrad、RMSProp、Adam等算法。

1、SGD存在的问题

? ? ? ? 使用相同的学习率对每个参数更新。需要选择足够小的学习率使得自变量在梯度较大的维度上不发散。这样会导致自变量在梯度较小的维度上迭代太慢了。动量法是为了让自变量的更新方向更加一致，从而降低发散可能。

2、AdaGrad

? ? ? 因为SGD存在不同的参数使用同一个学习率会造成一些问题，有的参数已经更新到最优值，另外一些参数还没有更新到最优值，这样在一次更新会造成之前已经更新到最优值的参数不稳定，因此在AdaGrad这个算法里就想给每个参数都以不同的学习率进行更新，在每个维度的梯度值来调整 各个维度上的学习率。

? ? ? 核心思想：利用了梯度的累计平方值，如果历史梯度频繁更新，那么一开始梯度会急剧减小，更新非常快。如果有些参数的更新比较慢，那么学习率比较大，更新的较快。

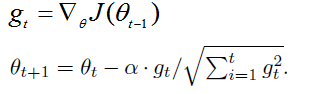
? ? 表示第t时间步的梯度，表示第t时间步的梯度平方。相比较SGD增加了分母：梯度平方累积和的平方根。能够累计各个参数的历史梯度平方，频繁更新，步长相对减少；稀疏梯度，更新步长相对较大。?

? ? ?优点：自动为不同参数适应不同的学习率。

? ? ?缺点：随着时间步的增加，分母项越大，最终导致学习率无法进行有效更新。一开始的分母较小，梯度急剧下降。

3、RMSProp

? ? ?还是为不同的参数分配不同的学习率，不过结合了梯度平方的指数移动平均数调节变化率的变化，使得在不稳定的目标函数中也能很好的收敛，能够解决梯度急剧下降的问题。

?

?

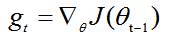
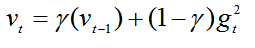
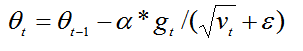
? ? γ是遗忘因子，这个最终要的改变就是给加上了系数，和SGD的动量有点像。为了让分母的变化稳定一些，梯度更新的时候只是更新梯度平方的期望（指数移动平均值）。这样变化会克服Adgrad梯度急剧减小的问题，在不稳定目标函数中表现的比较好。

4、AdaGrad和RMSProp

? ? ?RMSProp是AdaGrad的改进版本，改进的是梯度急剧减小的问题，防止在最后学习率太小，梯度难以更新的问题。举个例子说明

? ? AdadGrad的学习率变化：0.1、0.05、0.025、0.00125...

? ?RMSProp的学习率变化：0.1、0.08 、0.06、0.05......

? ?直观的可以看出来RMSProp学习率变化的缓慢一些，最后也很难学习率非常小而不能达到最优化。

5、Adam

? ? ?结合了动量和RMSProp两种优化算法的优点，对梯度的一阶矩估计（梯度的均值）和二阶矩估计（梯度的方差），进行综合考虑，计算出更新的步长。

? ?

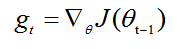
计算t时间步的梯度

?

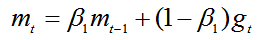
计算梯度的指数移动平均值，考虑之前时间步的梯度动量。

?

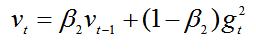
计算梯度平方的指数移动平均值，考虑之前时间步的梯度平方的影响。

?

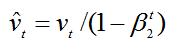
初始化都会偏向0，尤其在训练阶段的初期，因此需要对梯度均值和梯度平方的均值进行偏差纠正

?

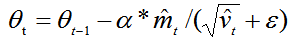
更新参数，

能够从梯度的均值和梯度平方的均值两个方面自适应地调节而不是直接由当前梯度决定。?

优点：

1、计算高效、非常快

2、适用于不稳定目标函数

3、适用于梯度稀疏的问题

4、超参数具有很好的解释性

5、自然的实现学习率的调整

?

REFERENCE:https://www.jianshu.com/p/aebcaf8af76e

?

?

?

?

?

?