行业新闻

改进的 A＊算法的路径规划（路径规划+代码+教程）_1

路径规划是人工智能领域中的重要问题之一，A* 算法作为一种常用的路径规划算法，通过启发式搜索在图形网络中找到最短路径。本文将介绍改进的 A* 算法，重点关注如何优化路径规划的效率和准确性。同时，提供代码示例和教程，帮助读者更好地理解和应用改进的 A* 算法。

A* 算法是一种经典的路径规划算法，它通过综合考虑节点的实际代价和启发式函数的估计值，从起始节点到目标节点搜索最短路径。然而，传统的 A* 算法在某些情况下存在搜索效率低下和得到次优解的问题。因此，我们提出了一种改进的 A* 算法，旨在优化路径规划的效率和准确性。

改进方法之一是引入跳点搜索（Jump Point Search）技术。跳点搜索通过检测直线路径上的阻塞点，直接跳过这些点，从而减少搜索空间。这种技术能够有效地剪枝，提高搜索效率。例如，在一个网格地图中，如果发现一个节点的邻居节点都是障碍物，就可以跳过这些邻居节点，直接搜索下一个可能的路径。这样可以大大减少搜索的节点数量，提高路径规划的效率。

另一个改进策略是优化启发式函数。传统的 A* 算法使用欧几里得距离或曼哈顿距离作为启发式函数，但在某些情况下可能不准确。我们可以根据实际问题的特点设计更合适的启发式函数，从而提高路径规划的准确性。例如，在机器人导航中，可以使用当前节点到目标节点的预估时间作为启发式函数，通过考虑实际行驶速度和交通状况，更准确地预测最短路径。

###############构造地图################
#宽高W，H。
class Array2D:
    #初始化
    def __init__(self,w,h):
        self.w=w
        self.h=h
        self.data=[]
        self.data=[[0.0 for y in range(h)]for x in range(w)]
 
    #显示地图
    def showArray2D(self):
        for y in range(self.h):
            for x in range(self.w):
                print(self.data[x][y],end=' ')
            print("")
    
    #获得任意节点信息 ，__getitem__()魔法函数作用为当实例化对象map进行map[key]操作上自动调用。
    def __getitem__(self, item):
        return self.data[item]

###############创建点类################
class Point:
    #初始化
    def __init__(self,x,y):
        self.x=x
        self.y=y
        
    #判断是否同一个点
    def __eq__(self, other):
        if self.x==other.x and self.y==other.y:
            return True
        return False
    
    #打印点信息
    def __str__(self):
        return "x:"+str(self.x)+",y:"+str(self.y)

在启发式搜索算法中， A算法是其中最为典型的代表，它在全局路径规划算法中，具有快速、高效和准确的优点，因此在智能车辆和工业机器人的路径规划问题上得到了广泛的应用。针对规划路径的需求和任务的要求，许多学者对传统 A算法进行改进，例如：路径的长度、规划效率和拐点数等方面。（下图为传统A*算法流程）

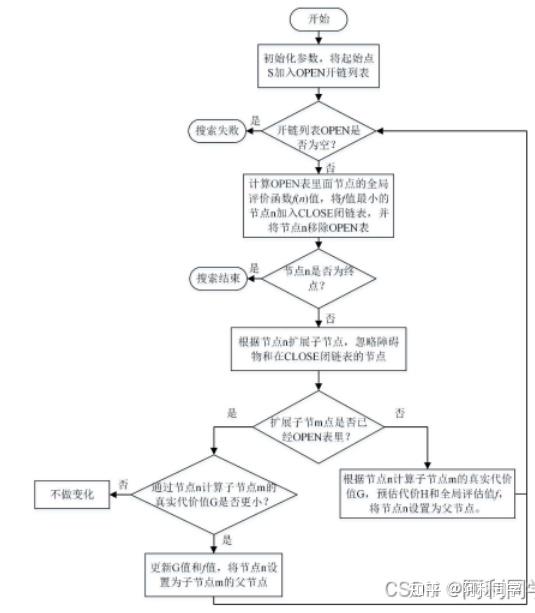
传统 A*算法缺点分析

虽然传统的 A算法在一些简单的场景具有一定的有效性，但是实际的用途中，环境复杂性对于算法实时的要求，传统的 A算法并无法满足要求。只有对传统算法的局限性进行深入了解分析才能更好的在传统方法之上进行更进一步的改进，因此本小节深入分析传统 A*算法的局限性和不足，具体有：

首先要意识到的是处理的是离散数据，而不是现实世界中的“连续”地形。采样的数字地形图像是真实地形的近似值，应该在一个理想的高分辨率采样。数字地形图像的分辨率越高，对真实地形的描述越逼真，寻径精度也越高。然而，在分辨率上存在一个上限，超过这个上限后，道路就不再更加精确，并且会不必要地增加寻径算法的运行时间。而且传统的建模方式只限定为可行驶区域和障碍物区域，然而

现实世界环境是及其复杂的，例如可行驶区域可区分为不同道路，沙地、草地、土质路面等等；障碍物也区分有树、行人、车辆建筑物等等。

为了找到从起始节点到目标节点的路径，我们必须定义一种选择后续节点的方式。我们可以从一个给定的位置移动到哪里？在现实世界中，一个人可以朝着喜欢的任何方向前进，但在数字地形图上，我们的选择更受限制。传统的 A*算法中有两种常见的方法：4 个邻接和 8 个邻接。4 个邻接限制移动在北、南、西、东四64 个主要风向。8 邻接的移动更自由，因为它除了 4 邻接的方向外，还可以在东北、西北、西南和东南方向移动。

在不同的任务要求中，有的任务要保证路径的最短，则设计预估代价小于真实代价，但是效率低下；有的任务要保证效率的高效，设计预估代价大于真实代价，但是规划的路径不是最优。

对于现实的环境场景，可能寻找道路的搜索空间非常大，这意味着必须采取措施确保内存不会耗尽，或者搜索不会花费过多的时间运行。即使是一个相对较小的300 × 300 像素的地形图也有 9 万个节点的搜索空间。

越野环境下的 A*算法

障碍物模型：

传统的 A*算法的构建方式中最普遍应用的是栅格法，其基本的思路是把智能车辆的工作空间分割为尺寸一致的网格，并通过数据矩阵来记录环境数据。常规的栅格算法把物理环境严格区分为自由区域和障碍物区域，从而使得数值矩阵能够简化为 0-1 矩阵，0 为自由空间，1 为障碍物空间。如假设智能车的工作空间为

R C? ，M 为数值矩阵，?表示所有的环境信息，则常规的环境模型可以表示为。

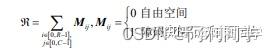
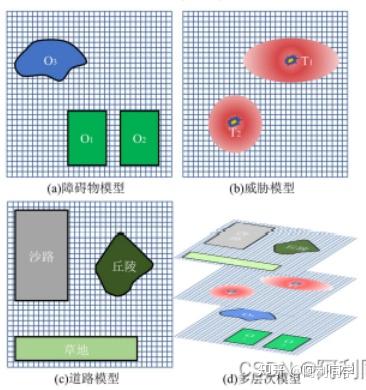
很明显，常规的栅格模型是无法模拟出真实复杂的越野环境，因此本文研究越

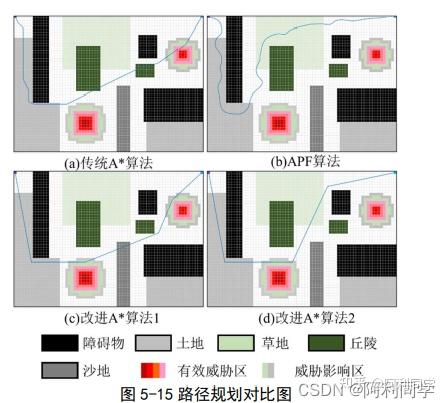
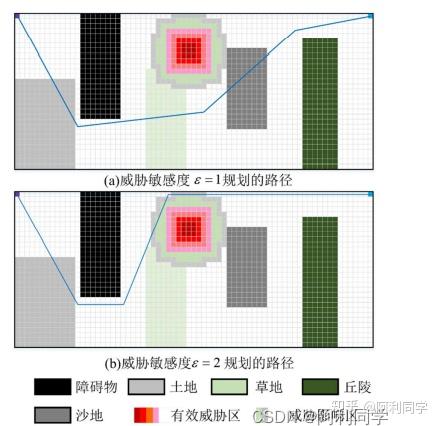
野环境的真实场景，建立多层次栅格模型，将越野环境模型细分为障碍物模型，威胁模型和道路模型如图所示：

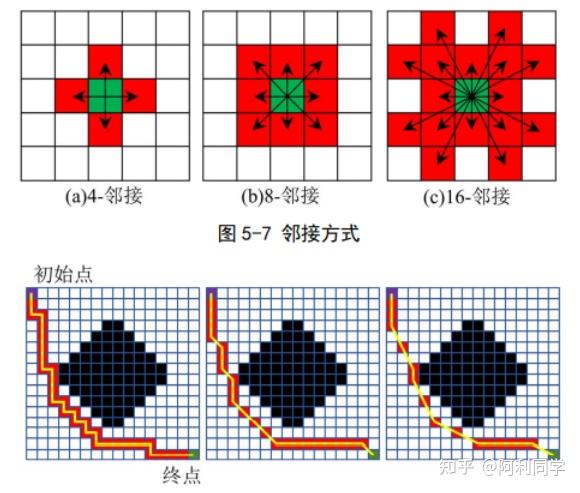
子节点优化选择策略

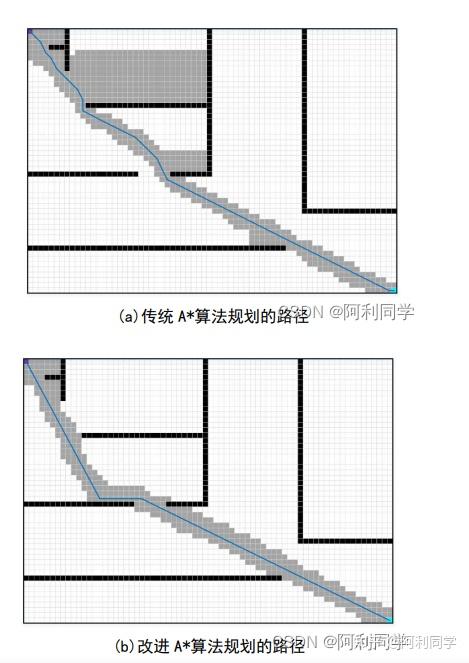
为了找到从起始点到终点的路径，需定义一种可以选择后续节点的方式。在A*算法中两种常见的方法为 4-邻接(见图 5-7(a))和 8-邻接 (见图 5-7(b))，但考虑到在复杂越野环境上，我们希望智能车辆允许更多的自由运动来更好规避危险，因此本文选择 16-邻接(见图 5-7?)。如图 5-8 所示，4-邻接规划的路径具有很多的直角拐点且路径最长，其次是 8-邻接规划的路径，而 16-邻接规划的路径平滑、拐点数少、路径短，适合复杂越野环境智能车的需求。

传统 A*算法在子节点选取上，仅考察子节点周围是否为障碍物，而未考察子节点与障碍物位置的相关性，从而规划出路线存在斜着通过障碍物栅格顶点的问题，导致车辆可能与障碍物发生碰撞。因为本文中所构建环境模型具有更危险的威胁物存在，所以优化了子节点的选择规则。

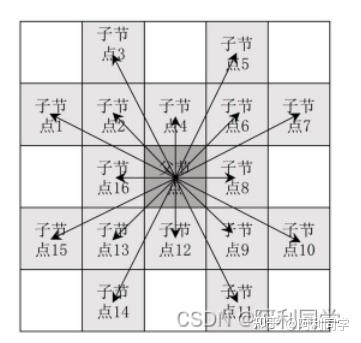
如图 5-9，为 16 个子节点分布图。本文结合越野环境栅格地图设计的子节点选择规则为：

1：若子节点 4 或子节点 12 具有威胁(在越野环境栅格地图?中值?1)，则子节点

2、子节点 6、子节点 3、子节点 5 或子节点 13、子节点 9、子节点 14、子节点11 不作为预选点。

3：若子节点 16 或子节点 8 具有威胁，则子节点 2、子节点 13、子节点 15、子节点 1 或子节点 6、子节点 9、子节点

4、子节点 7 不作为预选点。

5、均无具威胁，则不做处理。优化子节点选择后，规划后的路径避开具有威胁栅格的顶点，避免智能车辆

###############创建A-Star类############
class AStar:
    
    # 描述AStar算法中的节点数据
    class Node:  
        #初始化
        def __init__(self, point, startPoint,endPoint, g=0,w=1,p=1):
            self.point=point  # 自己的坐标
            self.father=None  # 父节点
            self.g=g       # g值，g值在用到的时候会重新算
            
            # 计算h值，采用曼哈顿距离
            #self.h=(abs(endPoint.x - point.x) + abs(endPoint.y - point.y)) * 10  
            
            #采用欧几里得距离
            #self.h=math.pow((math.pow((endPoint.x - point.x),2) + math.pow((endPoint.y - point.y),2)),0.5)*10
            
            #采用对角距离
            pp=(1-p)+0.2*math.exp((math.pow((math.pow((endPoint.x - point.x),2) + math.pow((endPoint.y - point.y),2)),0.5))/(math.pow((math.pow((endPoint.x - startPoint.x),2) + math.pow((endPoint.y - startPoint.y),2)),0.5)))
            Diagonal_step=min((endPoint.x - point.x),(endPoint.y - point.y))
            straight_step=(abs(endPoint.x - point.x) + abs(endPoint.y - point.y)) - 2*Diagonal_step
            self.h=(straight_step + math.pow(2,0.5)*Diagonal_step)*10*pp
            #print(pp)


            
    #初始化A-start
    def __init__(self, map2d, startPoint, endPoint, passTag=1.0):#map2d地图信息，startPoint起点, endPoint终点, passTag=1.0为不可行驶区域

        # 开启表
        self.openList=[]
        # 关闭表
        self.closeList=[]
        # 寻路地图
        self.map2d=map2d
        # 起点终点
        if isinstance(startPoint, Point) and isinstance(endPoint, Point):
            self.startPoint=startPoint
            self.endPoint=endPoint
        else:
            self.startPoint=Point(*startPoint)
            self.endPoint=Point(*endPoint)
 
        # 不可行走标记
        self.passTag=passTag
 
    def getMinNode(self):
        """
        获得openlist中F值最小的节点
        :return: Node
        """
        currentNode=self.openList[0]
        for node in self.openList:
            if node.g + node.h < currentNode.g + currentNode.h:
                currentNode=node
        return currentNode#返回最小代价的点