一滴水有多大？

俗话说“水滴石穿”，倒悬的水滴向下滴落是生活中常见的物理现象，那么一滴水有多大呢？看似简单的问题其实很不容易回答，这里面涉及到了非常多的物理。

首先我们先来思考一下水滴为什么能悬挂在平面上（例如天花板，玻璃等），答案是表面张力，液体的表面都有收缩的趋势，用更物理的语言描述就是，液体的表面上，长度为 的线上的张力为：

其中 叫做表面张力系数，常温下的水表面张力系数约为 ，如下图所示，正是表面张力抵消了水滴的重力，使得水滴可以悬挂在介质表面。

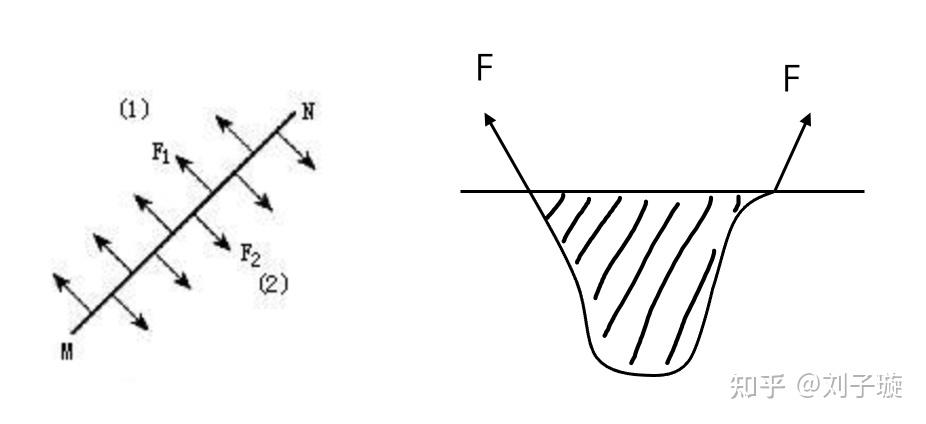
那么水滴有多大呢？这需要我们求解水滴的形状，在此之前我们可以先做一下量级估算，假设水滴是一个半径为 的半球形，水滴最大时张力等于重力，我们可以列出受力平衡方程：

由此估算出水滴的半径 ，代入数据约为 5mm，体积约为0.2mL，量级上的估计已经比较符合实际了。

求解水滴的形状有两种思路，一种是解Young-Laplace方程，另一种是用变分法求解，变分法就不介绍了，这里主要介绍Young-Laplace方程：

是液面两侧的压强差， 和 是液面的两个主曲率半径，即互相垂直的两个法平面和液面的交线的曲率半径，如下图所示：

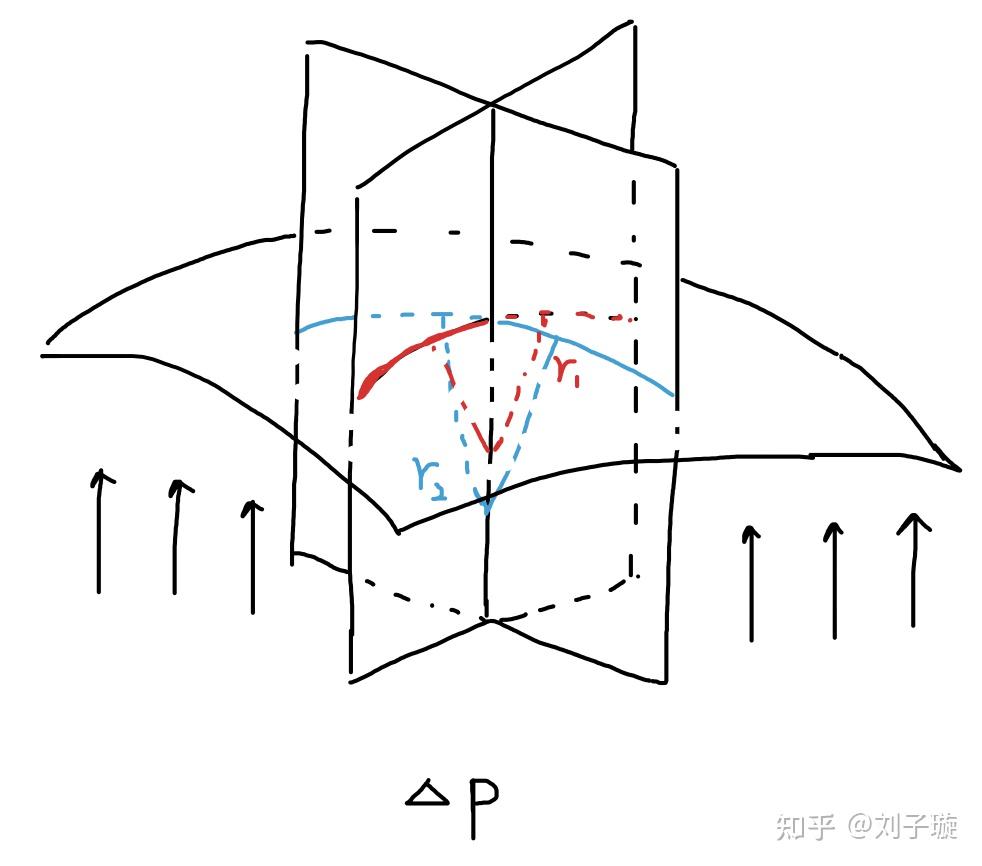
这个公式的证明需要微分几何的知识，这里就不多介绍了。总之这个公式告诉我们，液面弯曲的越厉害，造成的压强增量 越大，对于球形液面，公式可以简化为：

接下来我们利用Young-Laplace方程来求解水滴形状，假设水滴悬挂在水平面上，根据对称性可知，水滴的形状一定是一个旋转体，所以我们假设高度 处水滴的半径为 ，则列出平衡方程：

其中 是 处的压强差， 是曲线 的曲率半径（向里为正，向外为负）：

是另一个垂直截面的截线的曲率半径：

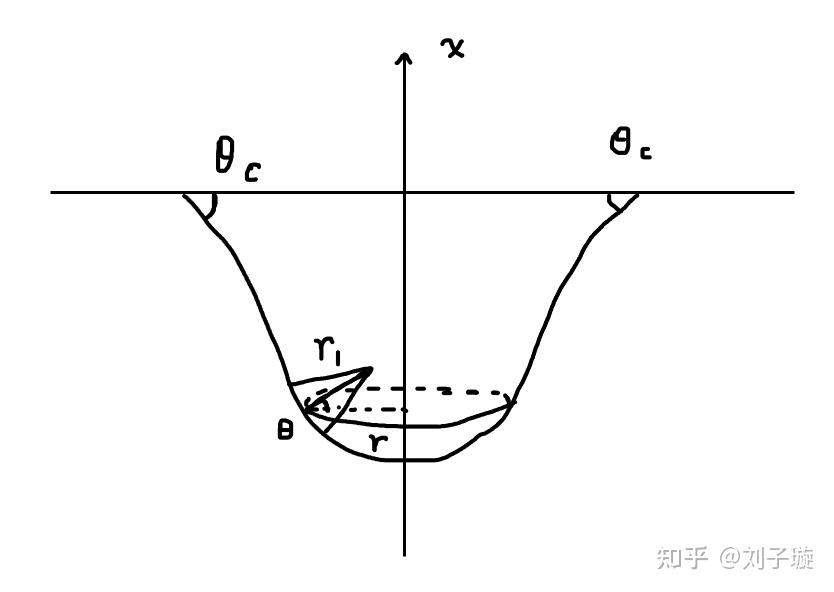
此外还需要水的体积恒定的约束条件：

以及水和介面接触角的边界条件：

是亲水介面，更容易附着水滴， 是疏水介面，不容易附着水滴。

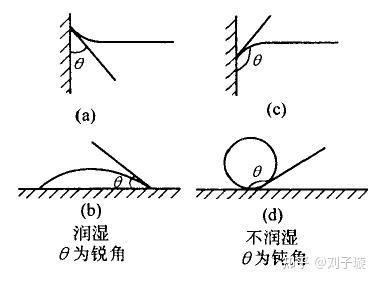
最终我们得到了一个关于 的二阶微分方程：

对该方程进行数值求解，我们发现有两个解满足边界条件，一个体积大，一个体积小，如下图所示：

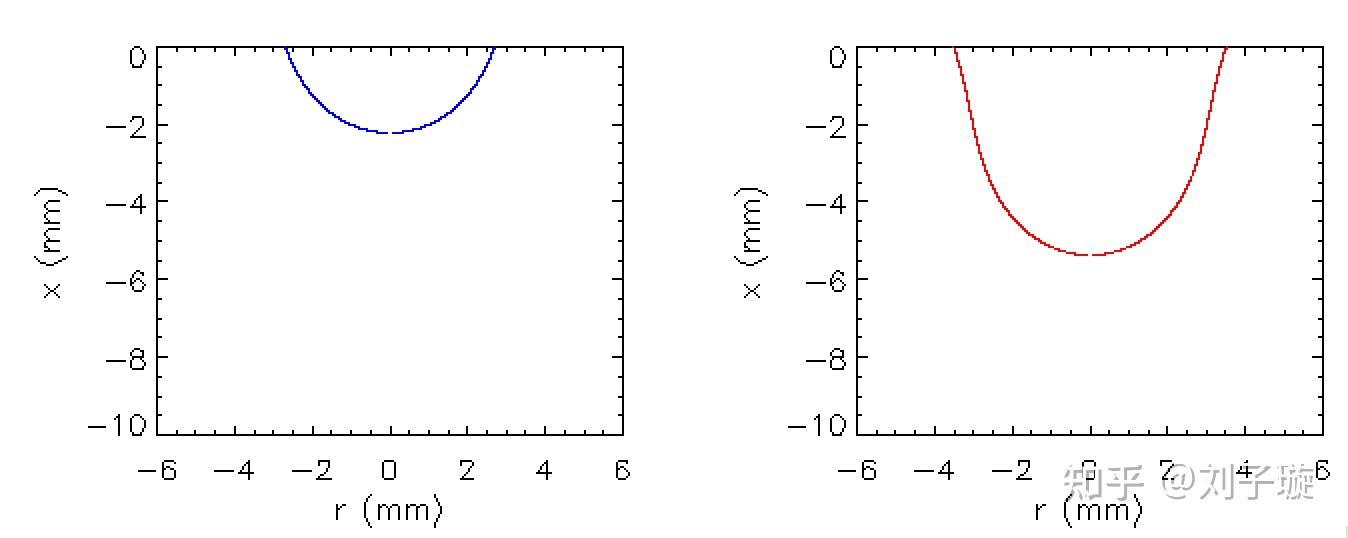
这是由 不单调造成的，因此我们还需要判断这两个平衡态是否是稳定的，严格的判定需要用到二阶变分，这里我们采取更简单的能量判据，考虑水滴的总能量包扩表面能和重力势能：

对于一个总体积为 的水滴，我们应该取能量较小的解为稳定平衡态。其实能量可以看做一个泛函，我们可以求解该泛函的极值，结合约束条件，利用拉格朗日乘子法就可以得到我们之前的二阶微分方程，有兴趣的读者可以自行尝试一下。

因此我们画出两个解对应的E-V图，如下图所示：

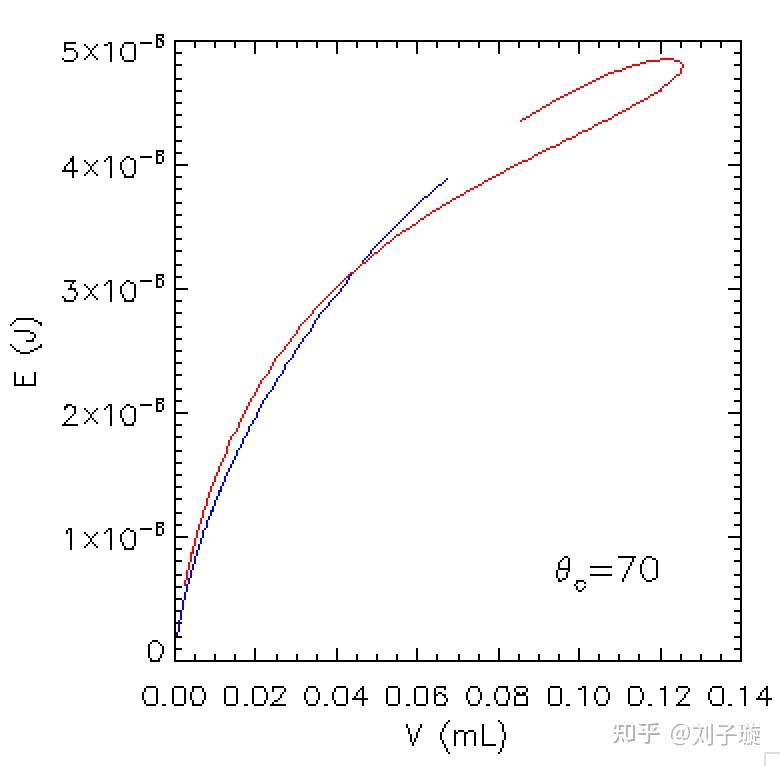
我们发现，当体积较小时，应该选取蓝色的解，当体积较大时，应该选择红色的解，图形还显示，水滴的体积有一个最大值，这表明在接触角 时，悬挂的水滴体积最大不会超过一个定值，大概在0.125mL左右，和我们之前的估算在一个量级。

接触角也会影响水滴体积的最大值，我们可以从下图中看到，接触角越大，水滴的最大体积越小，即越亲水的介面可以挂住更大的水滴，这也符合我们的生活经验。

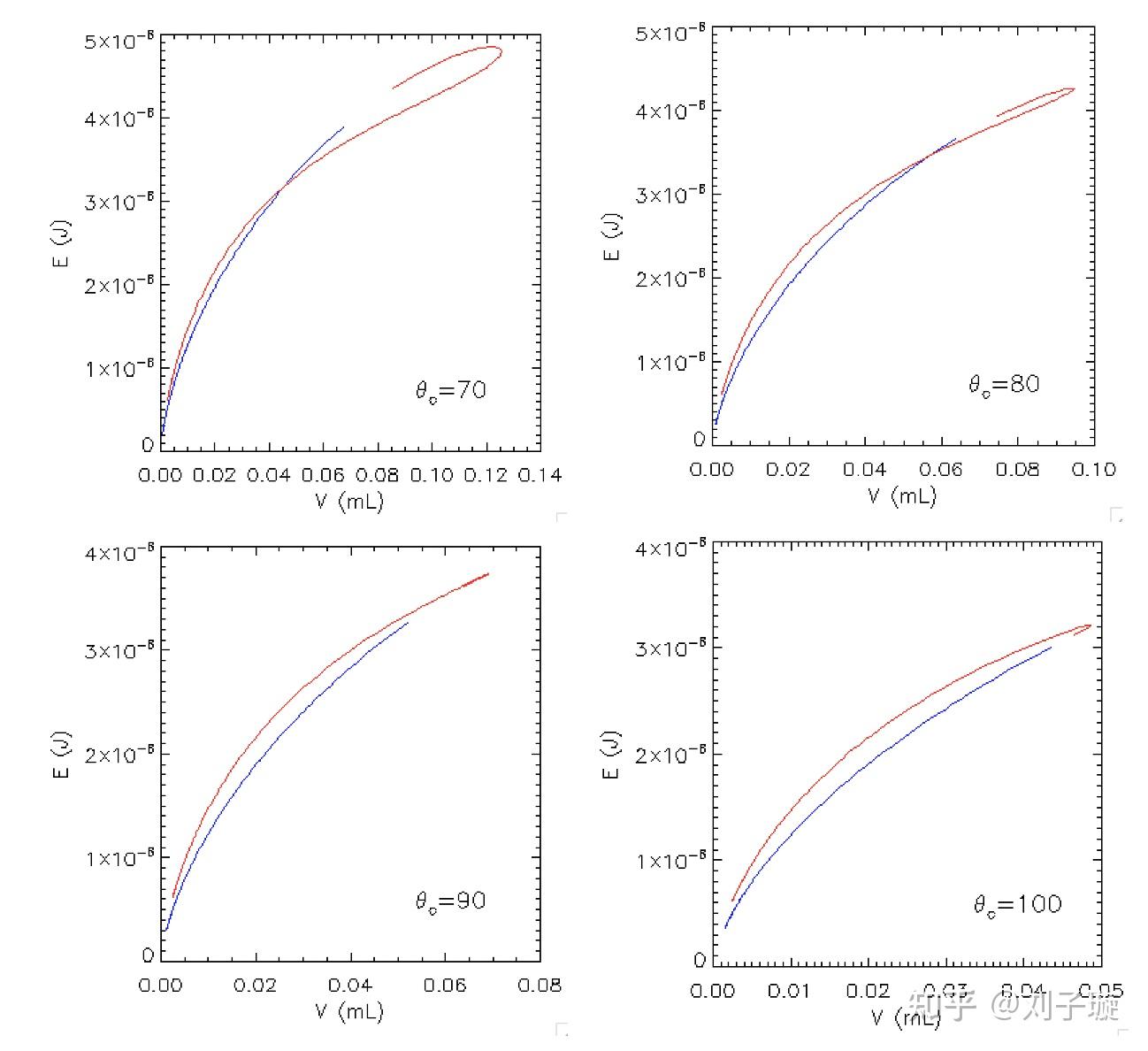
我们通过求解Young-Laplace方程研究了悬挂的水滴的形状和大小，发现水滴的临界大小普遍在0.1mL的量级，且随着接触角的增大而减小。

更新一下

之后又重新计算了一下这个问题，我发现其实不止两个解，随着水珠底部压强的变大，解的个数会越来越多，最后变成糖葫芦形状：

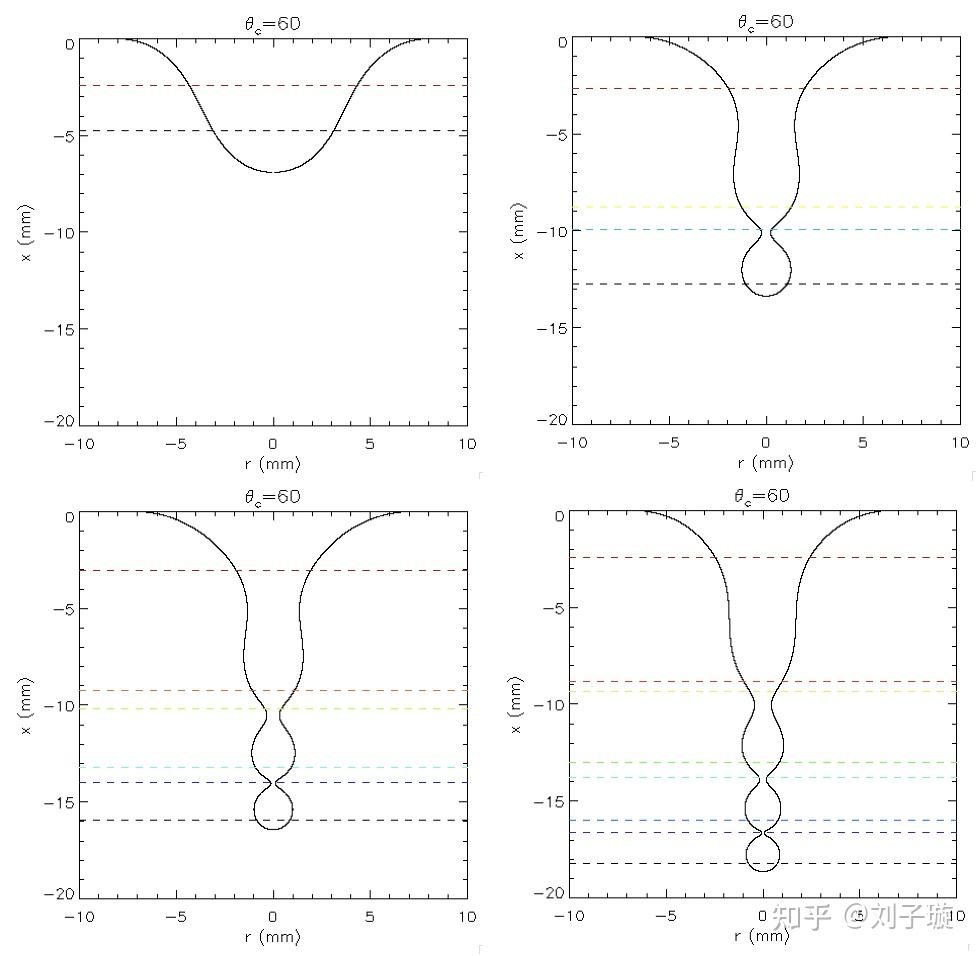
虽然之后的解看起来都不像是稳定解，但我们有必要用能量来验证一下：

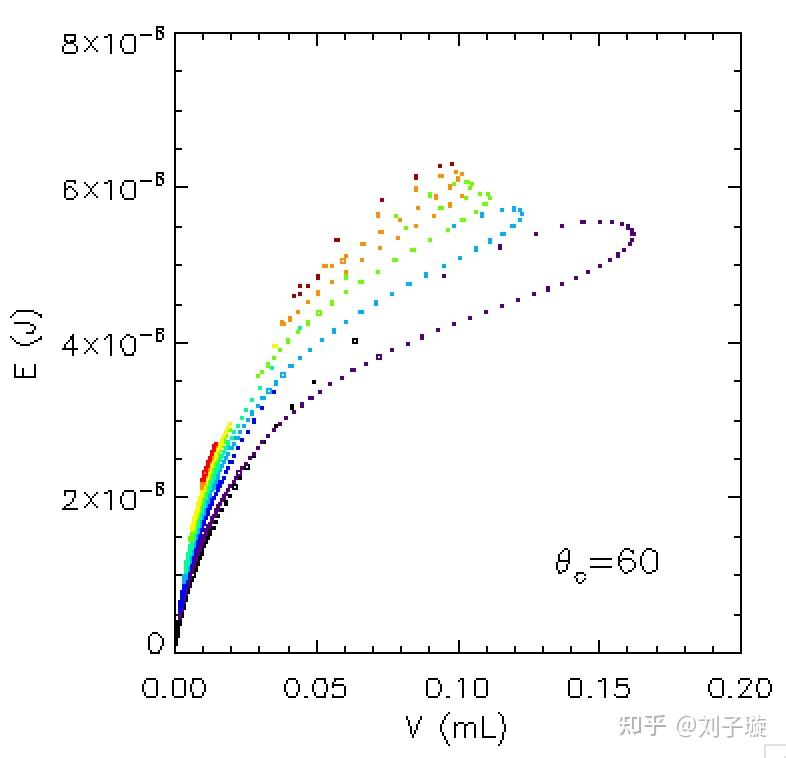
可以看出，对于体积相同的解来说，位置高的解能量都很大，因此都是不稳定的，只有最低和第二低的解才有可能是稳定的，最后我们可以计算并画出水滴的最大体积 和接触角 的关系：

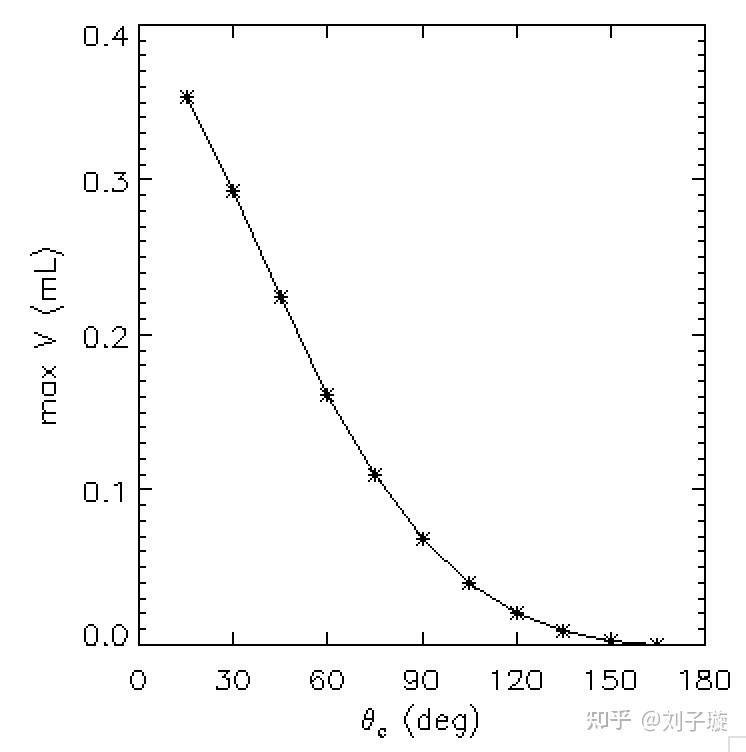
可以看出水滴的最大体积随着接触角增大而减小，最大不超过0.4mL，对于玻璃来说，接触角一般在40-70°之间，因此对应的水滴大小一般在0.1-0.2 mL之间，我们还可以利用已知物理量构造一个无量纲量：

我们就可以得到任意液滴的临界体积随接触角的变化：

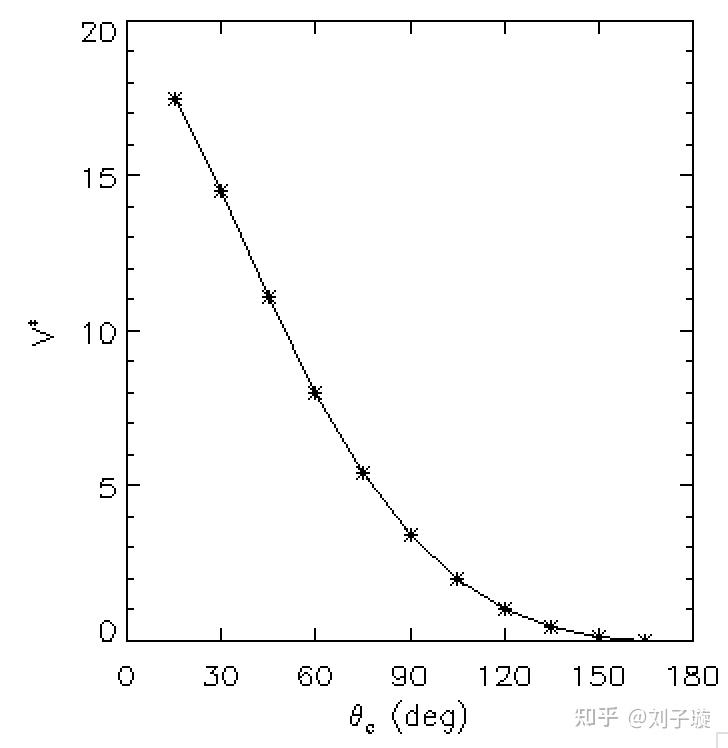
可以看到 的上限不超过20，随着接触角的变大，逐渐变为0。根据无量纲量的表达式我们还可以看出，表面张力系数越小、密度越大的液体，相同的接触角下其临界体积越小，这解释了为什么肥皂水在玻璃上的的液滴看起来比水滴小，因为肥皂水的表面张力系数比水小。