Adam 优化算法详解

据牛津字典的定义，优化是指最好或最有效地利用一种情况或资源，或者简单地使自己的事物达到最佳状态的行为。 通常，如果可以对某事进行数学建模，则很有可能可以对其进行优化。 这在深度学习领域起着至关重要的作用（可能是整个人工智能），因为您选择的优化算法可能是在数分钟，数小时或数天（有时甚至是数周）内获得高质量结果的区别。

在这篇文章中，我们将阐述：

1. 什么是Adam Optimizer？
2. 在深度学习模型中使用Adam进行优化有什么好处？
3. Adam如何工作？

Adam Optimizer是对SGD的扩展，可以代替经典的随机梯度下降法来更有效地更新网络权重。

请注意，Adam这个名字并不是首字母缩写词，实际上，作者（OpenAI的Diederik P. Kingma和多伦多大学的Jimmy Lei Ba）在论文中指出，该论文首次在ICLR 2015上作为会议论文发表，标题为Adam: A method for Stochastic Optimization, that the name is derived from adaptive moment estimation.。

作者毫不犹豫地列出了将Adam应用于非凸优化问题的许多迷人好处，我将继续分享以下内容：

简单地实现（我们将在本文的稍后部分中实现Adam，并且您将直接看到如何利用强大的深度学习框架以更少的代码行使实现变得更加简单。）

1. 计算效率高
2. 很少的内存需求
3. 梯度的对角线重缩放不变（这意味着亚当将梯度乘以仅带正因子的对角矩阵是不变的，以便更好地理解此堆栈交换）
4. 非常适合数据和/或参数较大的问题
5. 适用于非固定目标
6. 适用于非常嘈杂和/或稀疏梯度的问题
7. 超参数具有直观的解释，通常需要很少的调整（我们将在配置部分中对此进行详细介绍）

简而言之，Adam使用动量和自适应学习率来加快收敛速度。

在解释动量时，研究人员和从业人员都喜欢使用比球滚下山坡而向局部极小值更快滚动的类比法，但从本质上讲，我们必须知道的是，动量算法在相关方向上加速了随机梯度下降，如 以及抑制振荡。

为了将动量引入我们的神经网络，我们将时间元素添加到过去时间步长的更新向量中，并将其添加到当前更新向量中。 这样可以使球的动量增加一定程度。 可以用数学表示，如下图所示。

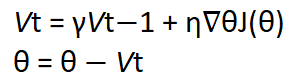
动量更新方法，其中θ是网络的参数，即权重，偏差或激活值，η是学习率，J是我们要优化的目标函数，γ是常数项，也称为动量。 Vt-1（注意t-1是下标）是过去的时间步长，而Vt（注意t是下标）是当前的时间步长。

动量项γ通常被初始化为0.9或类似于Sebastian Ruder的论文《An overview of gradient descent optimization algorithm》中提到的项。

通过将学习率降低到我们在AdaGrad，RMSprop，Adam和AdaDelta中看到的预定义时间表(schedule)，可以将自适应学习率视为训练阶段的学习率调整。这也称为学习率时间表 有关该主题的更多详细信息，Suki Lau撰写了一篇有关该主题的非常有用的博客文章，称为“ Learning Rate Schedules and Adaptive Learning Rate Methods for Deep Learning.”。

在不花太多时间介绍AdaGrad优化算法的情况下，这里将解释RMSprop及其在AdaGrad上的改进以及如何随时间改变学习率。

RMSprop（即均方根传播）是由Geoff Hinton开发的，如《An Overview of Gradient Descent Optimization Algorithms》所述，其目的是解决AdaGrad的学习率急剧下降的问题。 简而言之，RMSprop更改学习速率的速度比AdaGrad慢，但是RMSprop仍可从AdaGrad（更快的收敛速度）中受益-数学表达式请参见下图

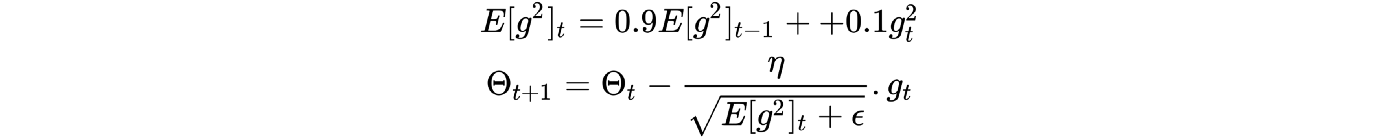
E[g2]t的第一个方程是平方梯度的指数衰减平均值。 Geoff Hinton建议将γ设置为0.9，而学习率η的默认值为0.001

这可以使学习率随着时间的流逝而适应，这很重要，因为这种现象也存在于Adam中。 当我们将两者（Momentum 和RMSprop）放在一起时，我们得到了Adam —下图显示了详细的算法。

如果你听过吴恩达老师的深度学习课程，吴恩达老师说过“Adam可以理解为加了Momentum 的 RMSprop” ，上图的公式就是吴恩达老师这句话的由来。

• Kingma, D and Ba, J . (2015) Adam: A method for Stochastic Optimization.
• Ruder, S. (2017) An overview of gradient descent optimization algorithms.
• Duchi, J et al. (2011) Adaptive Subgradient Methods for Online Learning and Stochastic Optimization.